欢迎访问『 博普智库 』制药人必备知识工具
1431 生物检定统计法
—、总则
生物检定法是利用生物体包括整体动物、离体组织、器官、细胞和微生物等评估药物生物活性的一种方法。它以药物的药理作用为基础,以生物统计为工具,运用特定的实验设计在一定条件下比较供试品和与其相当的标准品或对照品所产生的特定反应,通过等反应剂量间比例的运算或限值剂量引起的生物反应程度,从而测定供试品的效价、生物活性或杂质引起的毒性。
生物检定统计法主要叙述应用生物检定时必须注意的基本原则、一般要求、实验设计及统计方法。有关品种用生物检定的具体实验条件和要求,必须按照该品种生物检定法项下的规定。
生物检定标准品 凡中国药典规定用生物检定的品种都有其生物检定标准品(S)。S都有标示效价,以效价单位(u)表示,其含义和相应国际标准品的效价单位一致。
供试品 供试品(T)或(U)是供检定其效价的样品,它的活性组分应与标准品基本相同。
AT或AU是T或U的标示量或估计效价。
等反应剂量对比 生物检定是将T和其S在相同的实验条件下同时对生物体或其离体器官组织等的作用进行比较,通过对比,计算出它们的等反应剂量比值(R),以测得T的效价PT。
R是S和T等反应剂量(dS、dT)的比值,即R=dS/dT。
M是S和T的对数等反应剂量(xS、xT)之差,即M=lgdS-lgdT=xS-xT。R=antilgM。
PT是通过检定测得T的效价含量,称T的测得效价,是将效价比值(R)用T的标示量或估计效价AT校正之后而得,即PT=AT•R或PT=AT•antilgM。
检定时,S按标示效价计算剂量,T按标示量或估计效价(AT)计算剂量,注意调节T的剂量或调整其标示量或估计效价,使S和T的相应剂量组所致的反应程度相近。
生物变异的控制 生物检定具有一定的实验误差,其主要来源是生物变异性。因此生物检定必须注意控制生物变异,或减少生物变异本身,或用适宜的实验设计来减小生物变异对实验结果的影响,以减小实验误差。控制生物变异必须注意以下几点:
(1)生物来源、饲养或培养条件必须均一。
(2)对影响实验误差的条件和因子,在实验设计时应尽可能作为因级限制,将选取的因级随机分配至各组。例如体重、性别、窝别、双碟和给药次序等都是因子,不同体重是体重因子的级,雌性、雄性是性别因子的级,不同窝的动物是窝别因子的级,不同双碟是碟间因子的级,给药先后是次序因子的级等。按程度划分的级(如动物体重),在选级时,应选动物较多的邻近几级,不要间隔跳越选级。
(3)按实验设计类型的要求将限制的因级分组时,也必须严格遵守随机的原则。
误差项 指从实验结果的总变异中分去不同剂量及不同因级对变异的影响后,剩余的变异成分,用方差(s2)表示。对于因实验设计类型的限制无法分离的变异成分,或估计某种因级对变异的影响小,可不予分离者,都并入s2。但剂间变异必须分离。
误差项的大小影响标准误SM和可信限❶(FL)。
不同的检定方法和实验设计类型,分别按有关的公式计算s2。
可靠性测验 要求在实验所用的剂量范围内,剂量或对数剂量的反应(或反应的函数)符合特定模型要求,且标准品与供试品的线性满足计算原理的要求,即满足系统适用性和样品适用性要求,方可按有关公式计算供试品的效价和可信限。如:
平行(直)线模型要求其在所用剂量范围内,对数剂量与反应(或反应的函数)呈直线关系,供试品和标准品的直线满足平行性要求;
四参数模型要求其在所用剂量范围内,对数剂量与反应(或反应的函数)呈S曲线形关系,供试品和标准品的S形曲线平行;
质反应资料要求其在所用剂量范围内,对数剂量与反应(或反应的函数)呈广义线性关系,供试品和标准品呈线性平行。
可信限和可信限率 可信限(FL)标志检定结果的精密度。M的可信限是M的标准误SM和t值的乘积(t・SM),用95%的概率水平。M+t・SM是可信限的高限;M+t・SM是可信限的低限。用其反对数计算得R和PT的可信限低限及高限,是在95%的概率水平下从样品的检定结果估计其真实结果的所在范围。
R或PT的可信限率(FL%)是用R或PT的可信限计算而得,为可信限的高限与低限之差除以2倍效价均值后的百分率。

计算可信限的t值是根据S2的自由度(f)查t值表而得。t值与f的关系见表一。
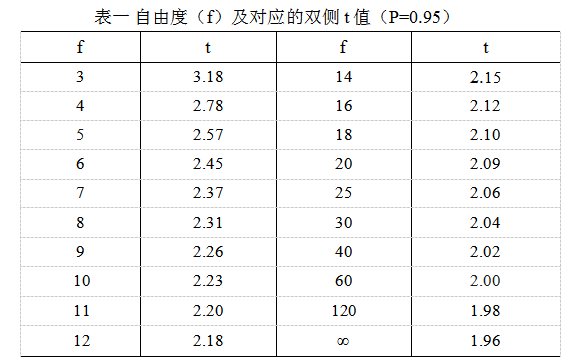
各品种的检定方法项下都有其可信限率的规定,如果检定结果不符合规定,可缩小动物体重范围或年龄范围等生物样本间的差异,或调整对供试品的估计效价或调节剂量,重复实验以减小可信限率。
对同批供试品重复试验所得n次实验结果(包括FL%超过规定的结果),可按实验结果的合并计算法算得PT的均值及其FL%作为检定结果。
➊ 可信限是可信推断的术语,现一般不再采纳。目前统计使用的是概率推断法,用置信区间表达变异性。中国药典所用的可信限与置信限所表述的意义一致。
二、直接测定法
直接测得药物对各个动物最小效量或最小致死量的检定方法。如洋地黄及其制剂的效价测定。
xs和xT为S和T组各只动物的对数最小致死量,它们的均值xs和xT为S和T组的等反应剂量,ns和nT为S和T组的动物数。
1.效价计算
按(1)~(3)式计算M、R和PT。
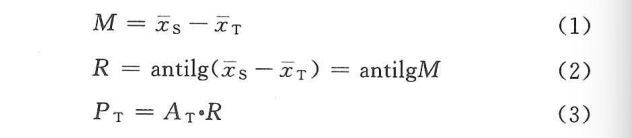
2.误差项及可信限计算
按(4)~(8)式计算s2、SM及R或PT的FL和FL%。
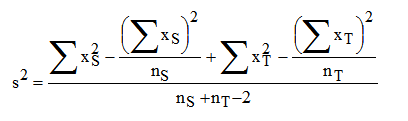
f=nS+nT-2,用此自由度查表一得t值。
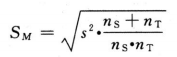
R的FL=antilg(M±t・SM) (6)
PT的FL=AT・antilg(M±t・SM) (7)

当两批以上供试品(T、U…)和标准品同时比较时,按(9)式计算S、T、U的合并方差s2。
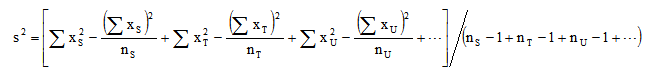
效价PT、PU…则是T、U分别与S比较,按(1)~(3)式计算。
3.实例
例1 直接测定法
洋地黄效价测定——鸽最小致死量(MLD)法
S为洋地黄标准品,按标示效价配成1.0u/ml的酊剂,临试验前稀释25倍。
T为洋地黄叶粉,估计效价AT=10u/g,配成1.0u/ml的酊剂,临试验前配成稀释液(1→25)。测定结果见表1-1。
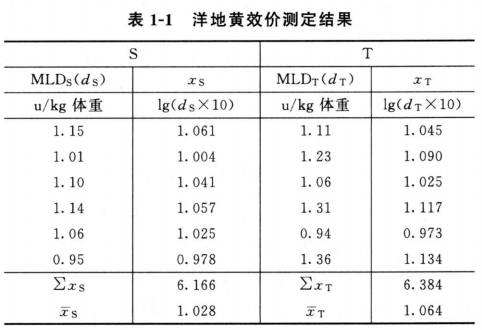
按(1)~(3)式:
M=1.028-1.064=-0.036
R=antilg(-0.036)=0.9204
PT=10×0.9204=9.20(u/g)
按(4)~(8)式计算s2、SM、PT的FL和FL%。

三、量反应平行线测定法
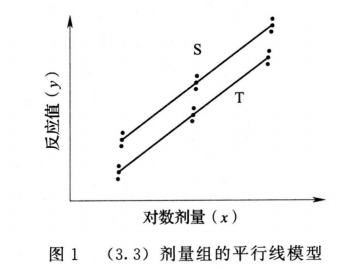
药物对生物体所引起的反应随着药物剂量的增加产生的量变可以测量者,称量反应。量反应检定用平行线测定法,要求在一定剂量范围内,S和T的对数剂量z和反应或反应的特定函数V呈直线关系,当S和T的活性组分基本相同时,两直线平行。量反应模型的原理见图1。
本版药典量反应检定主要用(2.2)法、(3.3)法、(4.4)法或(2.2.2)法、(3.3.3)法、(4.4.4)法,即S、T(或U)各设2个、3个或4个剂量组,统称(k・k)法或(k・k・k)法;如果S和T的剂量组数不相等,则称(k・k’)法;前面的k,代表S的剂量组数,后面的k或k’代表T的剂量组数。一般都是按(k・k)法实验设计,当S或T的端剂量所致的反应未达阈值,或趋于极限,去除此端剂量后,对数剂量和反应的直线关系成立,这就形成了(k・k’)法。例如(3.3)法设计就可能形成(2.3)法或(3.2)法等。因此,(k•k’)法中的k只可能比k’多一组或少一组剂量。(k・k’)法的计算结果可供重复试验时调节剂量或调整供试品估计效价时参考。无论是(k・k)法、(k・k’)法或(k・k・k)法,都以K代表S和T的剂量组数之和,故K=k+k或K=k+k’或K=k+k+k。
本版药典平行线测定法的计算都用简算法,因此对各种(k・k)法要求:
(1)S和T相邻高低剂量组的比值(r)要相等,一般r用(1∶0.8)~(1∶0.5),设lgr=I。
(2)各剂量组的反应个数(m)应相等。
1.平行线测定的实验设计类型
根据不同的检定方法可加以限制的因级数釆用不同的实验设计类型。本版药典主要用下面三种实验设计类型。
(1)随机设计 剂量组内不加因级限制,有关因子的各级随机分配到各剂量组。本设计类型的实验结果只能分离不同剂量(剂间)所致变异,如绒促性素的生物检定。
(2)随机区组设计 将实验动物或实验对象分成区组,一个区组可以是一窝动物、一只双碟或一次实验。在剂量组内的各行间加以区组间(如窝间、碟间、实验次序间)的因级限制。随机区组设计要求每一区组的容量(如每一窝动物的受试动物只数、每一只双碟能容纳的小杯数等)必须和剂量组数相同,这样可以使每一窝动物或每一只双碟都能接受到各个不同的剂量。因此随机区组设计除了从总变异中分离剂间变异之外,还可以分离区组间变异,减小实验误差。例如抗生素杯碟法效价测定。
(3)交叉设计 同一动物可以分两次进行实验者适合用交叉设计。交叉设计是将动物分组,每组可以是一只动物,也可以是几只动物,但各组的动物只数应相等。标准品(S)和供试品(T)对比时,一组动物在第一次试验时接受S的一个剂量,第二次试验时则接受T的一个剂量,如此调换交叉进行,可以在同一动物身上进行不同试品、不同剂量的比较,以去除动物间差异对实验误差的影响,提高实验精确度,节约实验动物。
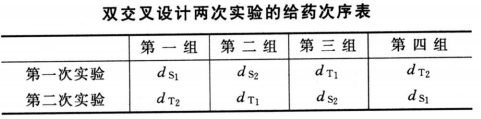
(2.2)法S和T各两组剂量,用双交叉设计,将动物分成四组;对各组中的每一只动物都标上识别号。每一只动物都按给药次序表进行两次实验。
2.平行线测定法的方差分析和可靠性测验
随机设计和随机区组设计的方差分析和可靠性测验
(1)将反应值或其规定的函数(y)按S和T的剂量分组列成方阵表 见表二。

方阵中,K为S和T的剂量组数和,m为各剂量组内y的个数,如为随机区组设计,m为行间或组内所加的因级限制;n为反应的总个数,n=mK。
(2)异常值剔除和缺项补足
异常值剔除 在同一剂量组内的各个反应值中,如出现特大或特小的反应值时,应进行异常值检验,以确定其是否应被剔除。检验异常值的方法很多,建议使用狄克森(Dixon)检验法和格拉布斯(Grubbs)检验法。
方法1 狄克森(Dixon)检验法
该法仅适于同组中反应值较少时,对其中可疑的异常反应值进行检验。该法假定在99%的置信水平下,一个有效的反应值被拒绝的概率仅有1%(异常值出现在单侧)。
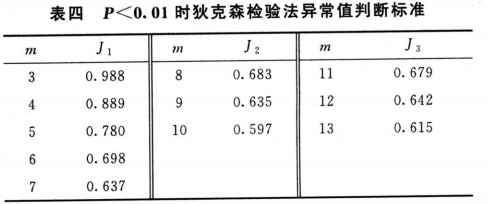
假定有同一组中m个观测反应值,按照由小到大的顺序进行排列,y1…ym。按表三中的公式对组内可疑的异常反应值计算J值。

如果J1、J2或J3中的计算值超出表四中给出的标准值,则判断为异常值,可考虑剔除。当同一组中的观察反应值数目大于13个时,请选用方法2。
对一个正态反应的样本,在99%置信水平下,差距不小于表四中J1、J2或J3的值时,其异常值出现在任一侧的概率P=0.01。
方法2 格拉布斯(Grubbs)检验法
该法既可用于同组反应值中的异常值检验,也可用于具有方差同质时的模型(如直线性模型或非直线性模型)中的残差法检测异常值。本法的计算原理如下。
找出本组数据中离样本均值最大的值yi,计算其标准化偏离值Z:

式中Y和S分别是该组数据的均值和标准差。对于使用平行线模型计算得到的残差,则Y=0;S是试验中的残差均值的平方根,即均方根误差。当|Z |大于使用下列公式得到的G值时,则认为 yi值属于99%置信水平下的一个统计异常值。

式中 m为本组数据的样本量;
t为在m-2自由度水平下,具有S标准偏差的t分,分布中100p%的单侧值。

缺项补足 因反应值被剔除或因故反应值缺失造成缺项,致m不等时,根据实验设计类型做缺项补足,使各剂量组的反应个数m相等。
随机设计 对缺失数据的剂量组,以该组的反应均值补入,缺1个反应补1个均值,缺2个反应补2个均值。
随机区组设计 按(13)式计算的值,补足缺项。
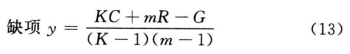
式中 C为缺项所在剂量组内的反应值总和;
R为缺项所在行的反应值总和;
G为全部反应值总和;
K为S和T的剂量组之和。
如果缺1项以上,可以分别以y1、y2、y3等代表各缺项,然后在计算其中之一时,把其他缺项y直接用符号y1、y2等当作未缺项代入(13)式,这样可得与缺项数相同的方程组,解方程组即得。
随机区组设计,当剂量组内安排的区组数较多时,也可将缺项所在的整个区组除去。
随机设计的实验结果中,如在个别剂量组多出1~2个反应值,可按严格的随机原则去除,使各剂量组的反应个数m相等。
不论哪种实验设计,每补足一个缺项,就需把s2的自由度减去1,缺项不得超过反应总个数的5%。
(3)方差分析 方阵表(表二)的实验结果,按(14)~(21)式计算各项变异的差方和、自由度(f)及误差项的方差(s2)。
随机设计 按(14)式、(15)式计算差方和(总)、差方和(剂间)。按(20)式计算差方和(误差)。按(18)式或(21)式计算s2。
随机区组设计 按(14)~(17)式计算差方和(总)、差方和(剂间)、差方和(区组间)、差方和(误差)。按(18)式或(19)式计算s2。


(4)可靠性测验 通过对剂间变异的分析,以测验S和T的对数剂量和反应的关系是否显著偏离平行直线。(2.2)法和(2.2.2)法的剂间变异分析为试品间、回归、偏离平行三项,其他(k・k)法还需再分析二次曲线、反向二次曲线等。
可靠性测验的剂间变异分析

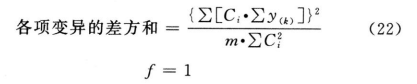
(k・k・k)法按(23)式、(24)式计算试品间差方和。
(2.2.2)法
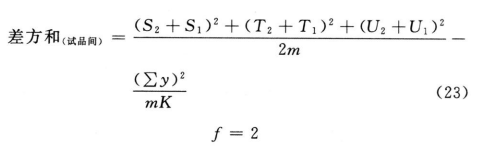
(3.3.3)法
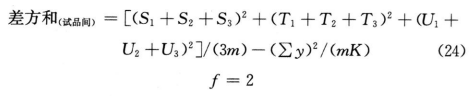


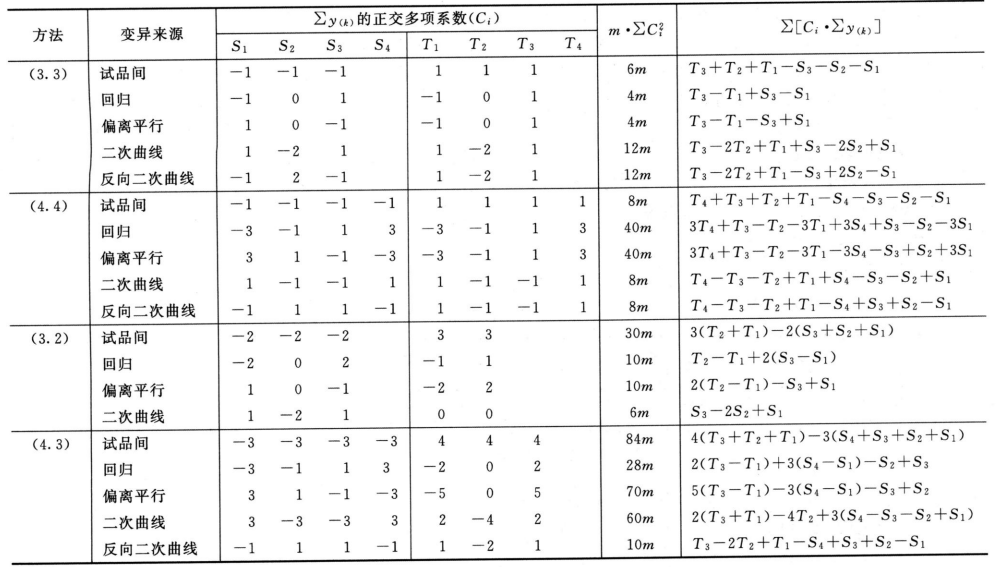

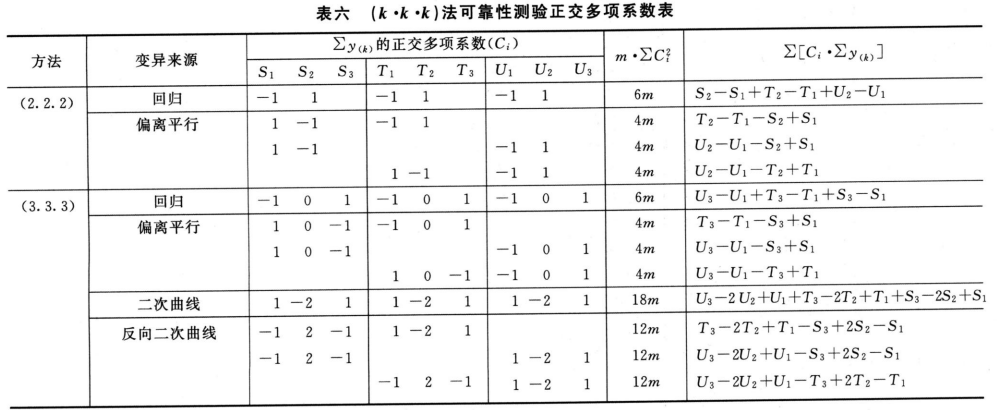
按(25)式计算差方和(偏离平行)及差方和(反向二次曲线)。
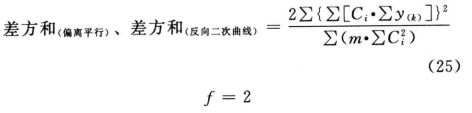
按(18)式计算各项变异的方差。
将方差分析结果列表进行可靠性测验。例如随机区组设
计(3.3)法可靠性测验结果列表,见表七。
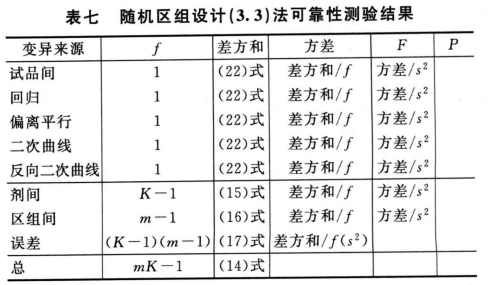
表七中概率P是以该变异项的自由度为分子,误差项(s2)的自由度为分母,查F值表(表八),将查表所得F值与表七F项下的计算值比较而得。当F计算值大于P=0.05或P=0.01的查表值时,则P<0.05或P<0.01,即为在此概率水平下该项变异有显著意义。
随机设计没有区组间变异项。
可靠性测验结果判断
可靠性测验结果,回归项应非常显著(P<0.01)。
(2.2)法、(2.2.2)法偏离平行应不显著(P>0.05)。
其他(k・k)法、(k・k・k)法偏离平行、二次曲线、反向二次曲线各项均应不显著(P>0.05)。
试品间一项不作为可靠性测验的判断标准,试品间变异非常显著者,重复试验时,应参考所得结果重新估计T的效价或重新调整剂量试验。
双交叉设计的方差分析和可靠性测验
(1)双交叉设计实验结果的方阵表 将动物按体重随机分成四组,各组的动物数(m)相等,四组的动物总数为4m。对四组中的每一只动物都加以识别标记,按双交叉设计给药次序表进行实验,各组的每一只动物都给药两次,共得2×4m个反应值。将S、T各两个剂量组两次实验所得反应值排列成表,见表九。
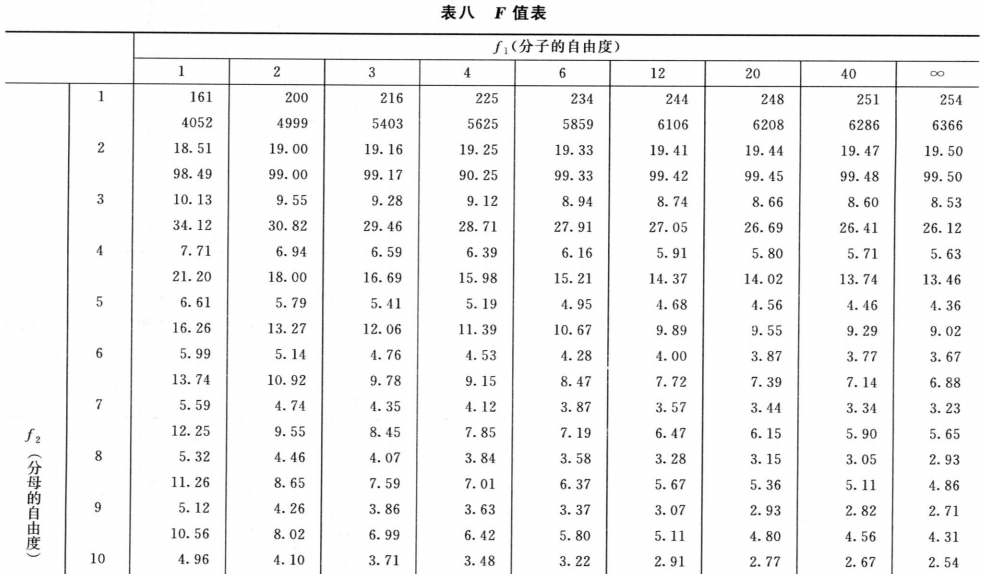
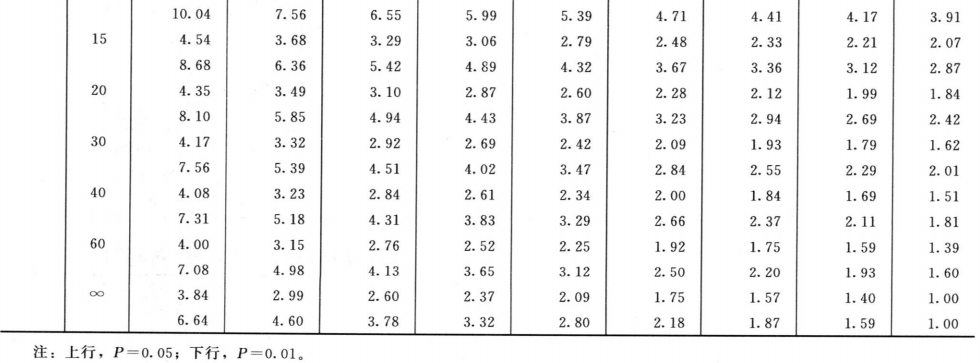
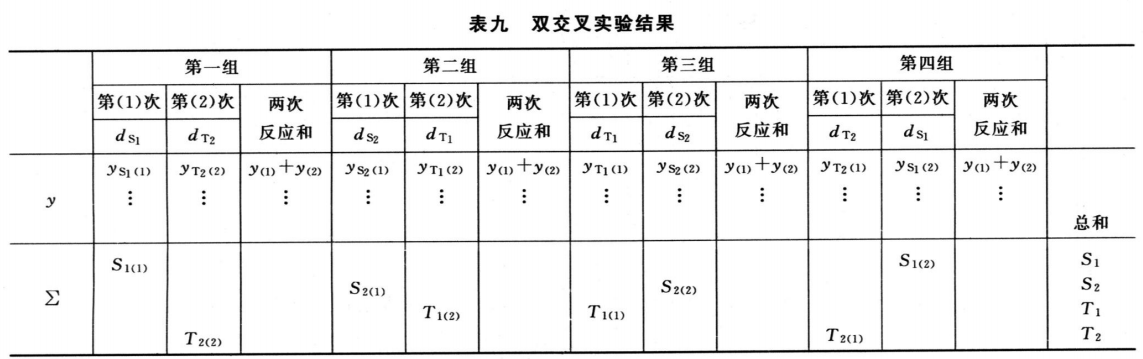
(2)缺项补足 表九中如有个别组的1个反应值因故缺失,均作该只动物缺失处理,在组内形成两个缺项。此时,可分别用两次实验中该组动物其余各反应值的均值补入;也可在其余三组内用严格随机的方法各去除1只动物,使各组的动物数相等。每补足一个缺项,误差(I)和误差(Ⅱ)的方差s2Ⅰ和s2Ⅱ的自由度都要减去1。缺项不得超过反应总个数的5%。同一组内缺失的动物不得超过1只。
(3)方差分析 双交叉设计的总变异中,包含有动物间变异和动物内变异。对表九的2×4m个反应值进行方差分析时,总变异的差方和(总)按(26)式计算。
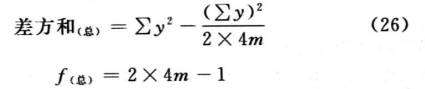
动物间变异是每一只动物两次实验所得反应值的和(表九每组动物的第三列)之间的变异,其差方和按(27)式计算。
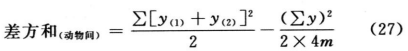
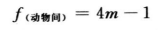
总变异中分除动物间变异,余下为动物内变异。
总变异的差方和减去动物间变异的差方和,再减去动物内各项变异的差方和,余项为误差(I)的差方和,按(28)式计算。

误差(I)的方差s2,用以计算实验误差SM、FL及进行动物内各项变异(表十中有*标记者)的F测验。
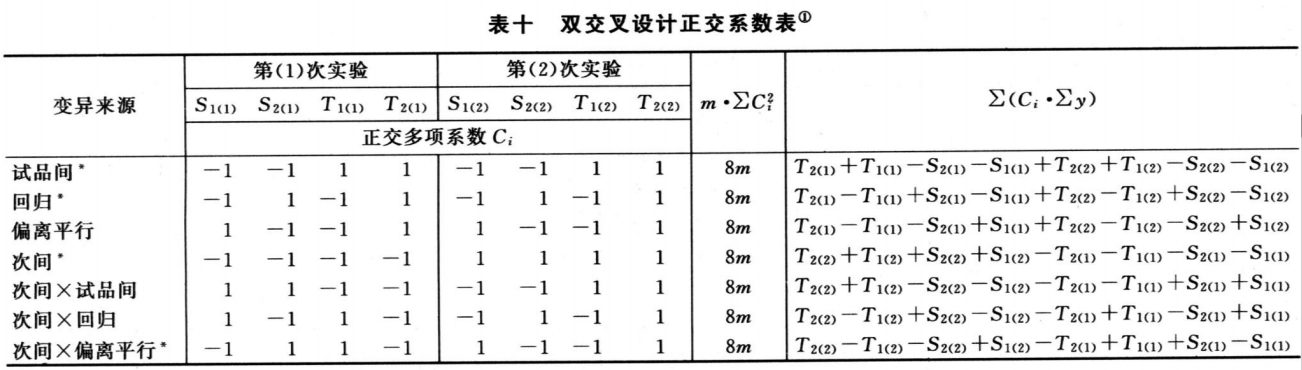
注:①各项变异的自由度均为1。有*号标记的四项为动物内变异,其余三项为动物间变异。
误差(Ⅱ)的差方和为动物间变异的差方和减去表十中其余三项变异(表十中无*标记者)的差方和,按(29)式计算。

误差(Ⅱ)的方差s2Ⅱ用以进行上述三项变异的F测验。
(4)可靠性测验 将方差分析及F测验的结果列表,如表十一。
表十一中的概率P,计算同表七,但表的上半部分是以s2Ⅱ的自由度为分母,表的下半部分以s2的自由度为分母,查F值表(表八),将查表所得的F值与表十一F项下的计算值比较而得。
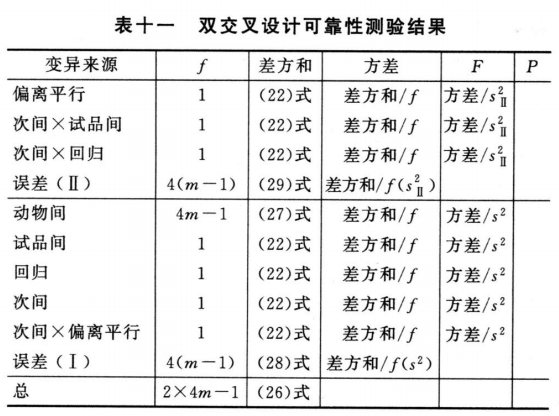
可靠性测验结果判断 回归、偏离平行、试品间三项的判断标准同(2.2)法。
次间×试品间、次间×回归、次间×偏离平行三项中,如有F测验非常显著者,说明该项变异在第一次和第二次实验的结果有非常显著的差别,对出现这种情况的检定结果,下结论时应慎重,最好复试。
3.效价(PT)及可信限(FL)计算
各种(k・k)法都按表十二计算V、W、D、A、B、g等数值,代入(30)~(33)式及(3)式、(8)式计算R、PT、SM以及R、PT的FL和FL%等。
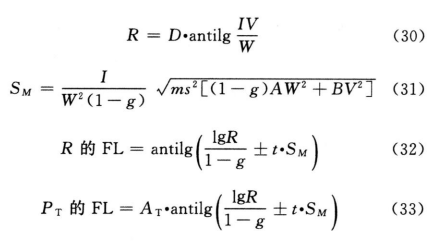
(2.2)法双交叉设计 计算方法同上述(2.2)法。双交叉设计各剂量组都进行两次试验,S和T每一剂量组的反应值个数为组内动物数的两倍(2m)。
(1)双交叉设计用S和T各组剂量两次实验所得有反应值之和(表九中的S1、S2、T1、T2)按表十二(2.2)法公式计算V、W、D数值。
(2)参照(31)式计算SM,因每只动物进行两次实验,式中m用2m代替,(2.2)法A=1,B=1,SM的公结式为
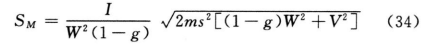
式中s2为表十一中误差(I)的方差;
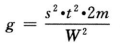
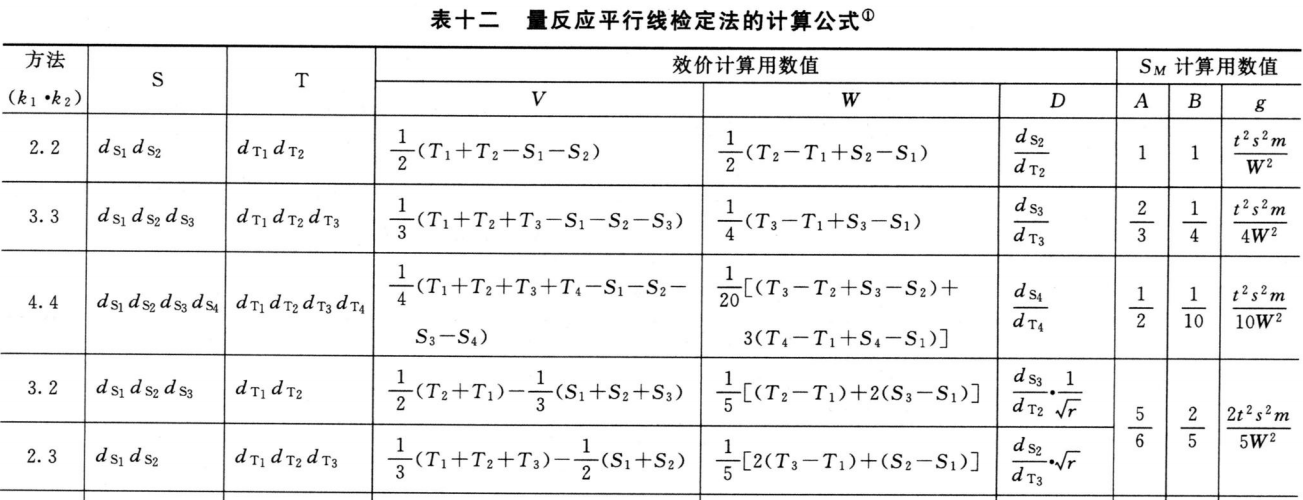

注:①表中dS、dT分别为S和T的剂量,下角1、2、3是顺次由小剂量到大剂量。
4.实例
例2 量反应平行线测定随机设计(3.3.3)法
绒促性素(HCG)效价测定——小鼠子宫法
S为绒促性素标准品
dS1:0.135u/鼠 dS2:0.225u/鼠 dS3:0.375u/鼠
T为绒促性素 估计效价AT:2500u/mg
dT1:0.135u/鼠 dT2:0.225u/鼠 dT3:0.375u/鼠
U为绒促性素粉针,标示量AU:500u/安瓿
dU1:0.144u/鼠 dU2:0.240u/鼠 dU3:0.400u/鼠
r=1∶0.6 I=0.222
反应(y):10g体重的子宫重(mg)
测定结果见表2-1。
(3.3.3)法,K=9;每组15只小鼠,m=15
(1)按(14)式、(15)式、(20)式计算各项的差方和
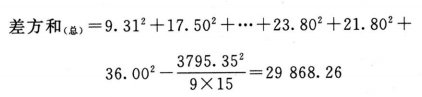

(2)剂间变异分析及可靠性测验 按(24)式及表六(3.3.3)法分析。
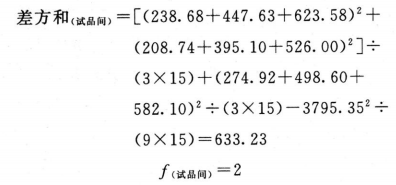
各项分析结果见表2-2、表2-3。
结论:回归非常显著,偏离平行、二次曲线、反向二次曲线均不显著,实验结果成立。
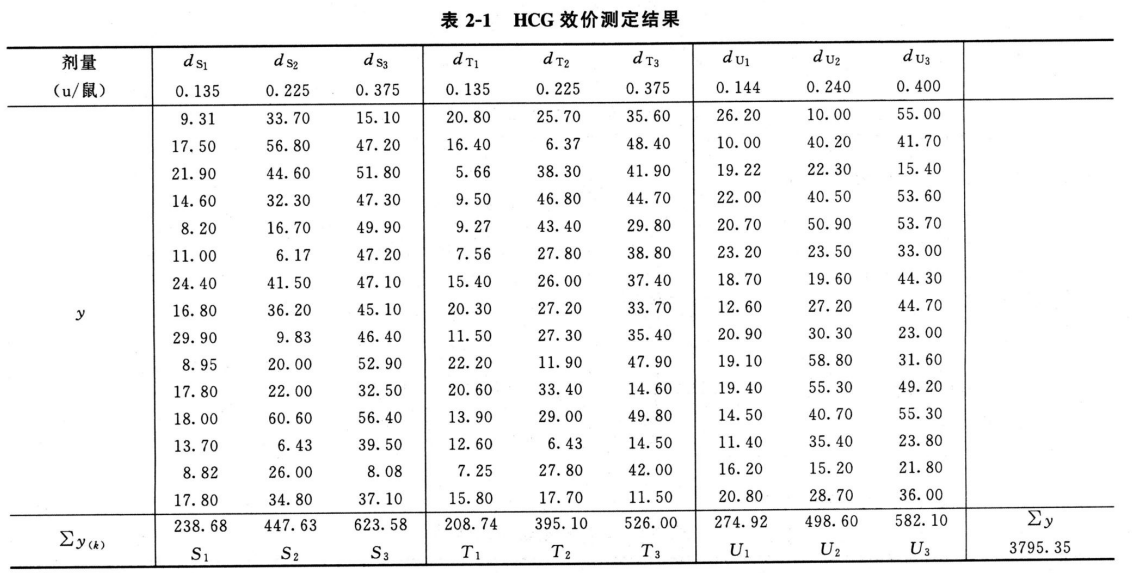

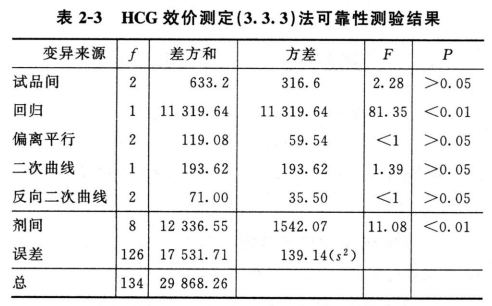
(3)效价(PT、PU)及可信限(FL)计算按表十二(3.3.3)法及(30)~(33)式、(3)式、(8)式计算。
r=1∶0.6 I=0.222
s2=139.14 f=126 t=1.98
PT及其FL计算:




与表2-3结果相同。
例3 量反应平行线测定随机区组设计(3.3)法
新霉素效价测定——杯碟法
S为新霉素标准品
稀释液dS1:8.0u/ml dS2:10.0u/ml dS3:12.5u/ml
T为新霉素 标示量AT:670u/mg
稀释液dT1:8.0u/ml dT2:10.0u/ml dT3:12.5u/ml
r=1∶0.8 I=0.0969
反应(y):抑菌圈直径(mm)
测定结果见表3-1。
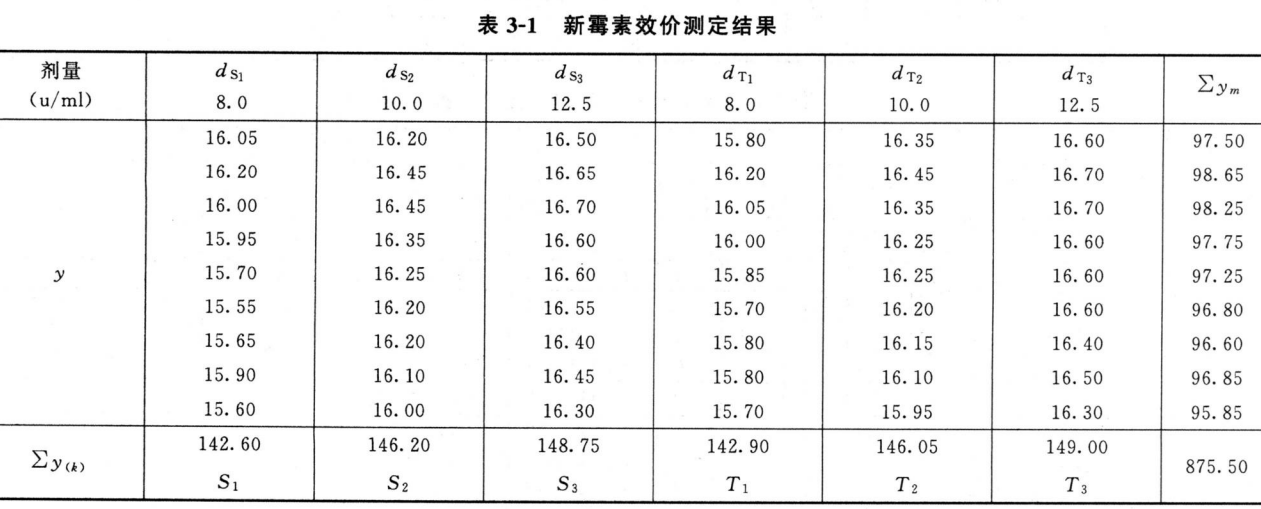
随机区组设计(3.3)法,K=6
不同双碟(碟间)是剂量组内所加的因级限制,共9个双碟,m=9。
(1)按(14)~(18)式计算各项差方和

(2)剂间变异分析及可靠性测验 按表五(3.3)法计算,结果见表3-2、表3-3。
结论:回归非常显著(P<0.01),偏离平行、二次曲线、反向二次曲线均不显著(P>0.05),实验结果成立。组内(碟间)差异非常显著(P<0.01),分离碟间差异,可以减小实验误差。
(3)效价(PT)及可信限(FL)计算 按表十二(3.3)法及(30)~(33)式、(3)式、(8)式计算。
r=1:0.8 I=0.0969 s2=0.006912 f=40
t=2.02(P=0.95)
PT及其FL计算:

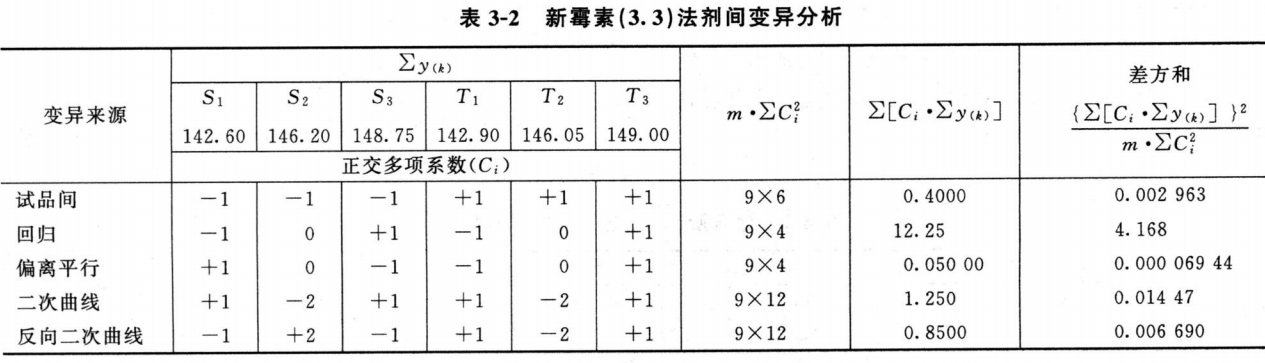
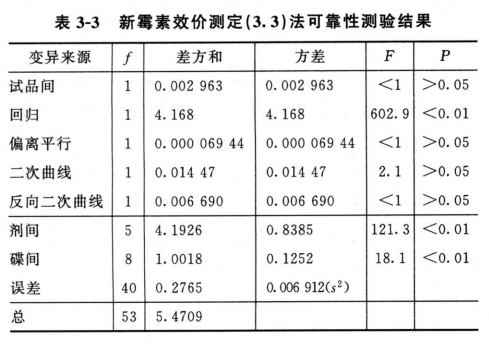
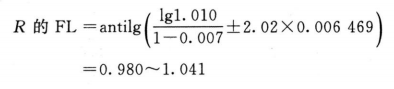

与表3-3结果相同。
例4 量反应平行线测定随机区组设计(2.2)法
缩宫素效价测定——大鼠离体子宫法
S为缩宫素标准品
dS1:0.0068u dS2:0.009u
T为缩宫素注射液 标示量AT:10u/ml
dT1:0.008u dT2:0.0106u
r=1:0.75 I=0.125
反应(y):子宫收缩高度(mm)
测定结果见表4-1。
随机区组设计(2.2)法,K=4。每组4个剂量为一区组,其给药次序为剂量组内所加因级限制。各剂量组均为5个反应,m=5。
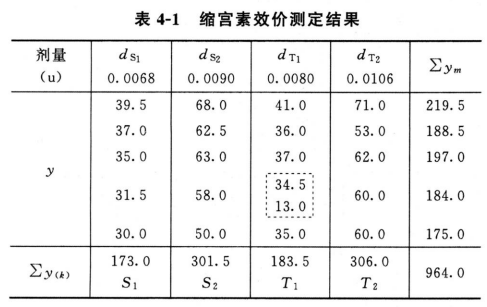
(1)特异反应处理 表4-1第三列第四行dT1的第4个数值特小,本例为随机区组设计按(10)式计算决定此值是否属特异值。
m=5 y1=13 y2=35 ym=41
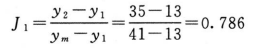
查表四,m=5时,J1=0.780,小于计算值0.786,故此值可以剔除。剔除后形成的缺项按(13)式补足。
C=149 R=149.5 G=929.5
K=4 m=5
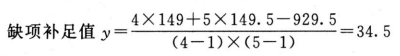
(2)按(14)~(18)式计算各项差方和补足了一个缺项,误差项的自由度按(17)式再减1。

(3)剂间变异分析及可靠性测验 按表五(2.2)法计算,结果见表4-2、表4-3。
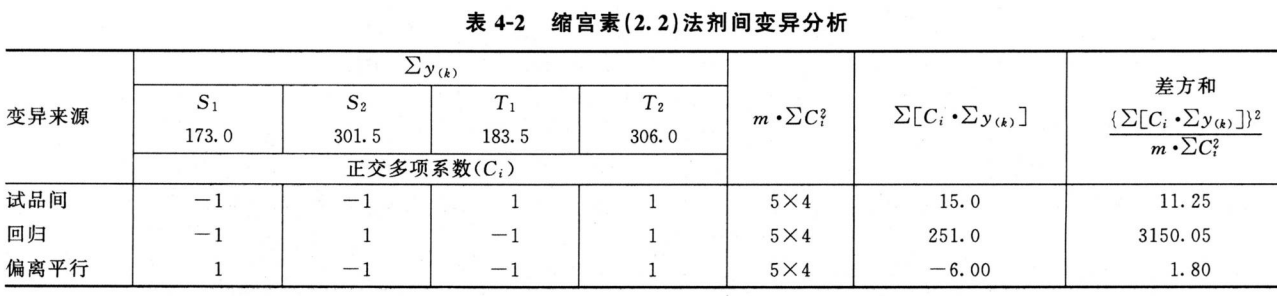
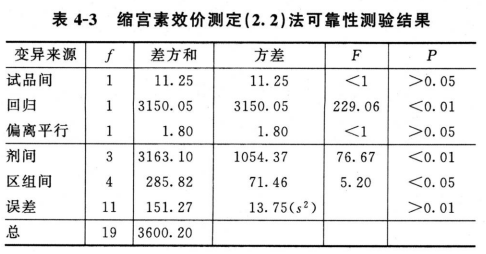
结论:回归非常显著(P<0.01),偏离平行不显著(P>0.05),实验结果成立。
区组间差异显著(P<0.05),分离区组间变异,可以减小实验误差。
缩宫素离体子宫效价测定,如区组间变异不显著,也可以不分离区组间变异,用随机设计方差分析法计算。
(4)效价(PT)及可信限(FL)计算 按表十二(2.2)法及(30)~(33)式、(3)式、(8)式计算。
r=1∶0.75 I=0.125 s2=13.75
f=11 t=2.20
PT及其FL计算:
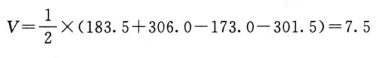

例5 量反应平行线测定(2.2)法双交叉设计
胰岛素效价测定——小鼠血糖法
S为胰岛素标准品
dS1:25mu/ml,0.25ml/鼠
dS2:50mu/ml,0.25ml/鼠
T为胰岛素 标示量AT:27u/mg
dT1:25mu/ml,0.25ml/鼠
dT2:50mu/ml,0.25ml/鼠
r=1∶0.5 I=0.301
反应值y:血糖值(mg%)
每组用鼠10只,m=10
测定结果按表九排列,见表5-1。
(1)方差分析 按(26)式、(27)式计算:

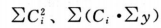
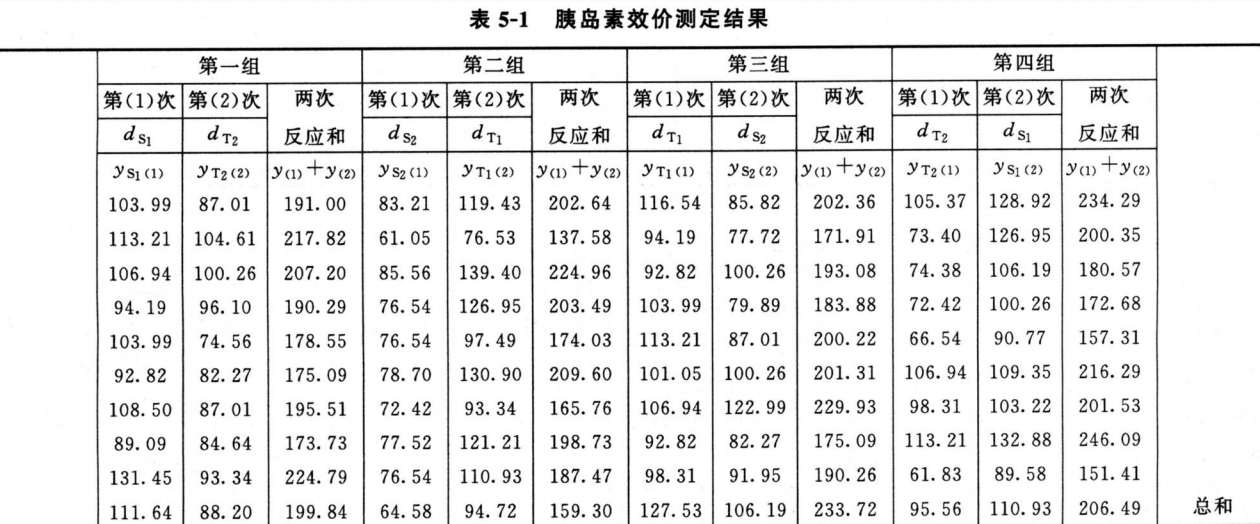

按(28)式、(29)式计算:
差方和(误差Ⅰ)=25865.8223-11320.6387-84.8102-9249.0855-1267.7893-369.4991=3579.9995
f(误差Ⅰ)=4×(10-1)=36
差方和(误差Ⅱ)=11320.6387-71.2720-215.7917-137.8388=10895.7362
f(误差Ⅱ)=4×(10-1)=36
结论:回归非常显著,偏离平行不显著,实验结果成立。两次实验间的差异非常显著,用双交叉设计可以消除实验间变异对实验误差的影响,提高实验的精确度。
(3)效价(PT)及可信限(FL)计算:
用表5-1的S1、S2、T1、T2,按表十二(2.2)法及(30)式、(32)~(34)式计算。
r=1∶0.5 I=0.301
s2=99.2778 f=36 t=2.03
PT及其FL计算:
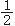
=41.185
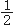
=-430.095

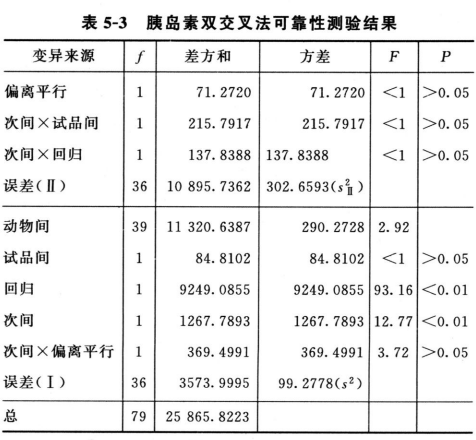
四、四参数回归计算法
四参数回归计算法系采用非线性模型进行量反应检定的一种统计分析方法。该法要求在一定剂量范围内,标准品(S)和供试品(T)的对数剂量x与反应值或反应值的特定函
数y呈“S”或反“S”形关系,可拟合成四参数逻辑斯蒂(logistic)回归方程,拟合曲线对称于拐点,上下各有一渐进线。当S和T的活性组分基本相同时,两拟合曲线平行。S形量反应四参数逻辑斯蒂(logistic)曲线模型图见图2。
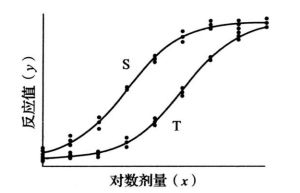
图2 S型量反应曲线的四参数逻辑斯蒂(logistic)模型
四参数逻辑斯蒂(logistic)曲线方程见(35)式:
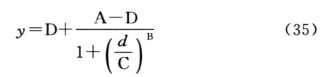
(36)式为另一种等价的方程形式:
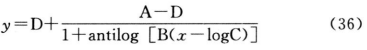
上述式中 y为反应值或反应值的特定函数;
d为标准品或供试品的各剂量;
x为对数剂量,x=logd;
A为d→0时的y(S形:下渐进线;反S形:上渐进线);
D为d→∞时的y(S形:上渐进线;反S形:下渐进线);

B为斜率因子(与EC50或ED50处曲线斜率相关)。
公式中对数的底数可取任一适用的底数,常以无理数e或10为底。A、B、C、D即为拟合曲线的4个特征性参数。本法主要以基于细胞的生物学活性测定法为例阐述四参数回归计算法的实验设计及运算过程。
1.实验设计
实验设计中要求S和T的剂量组数(n)应相等,每个剂量组反应值的个数(m)也应相等,且每个重复数应为独立重复。每组剂量间隔一般呈连续的等比稀释,也可采用非连续的独立稀释。实验过程中,应避免使用有严重位置效应的细胞孔,如会产生边缘效应的外周孔,S和T加样位置应尽量遵循随机、均衡排列的原则,也可选用随机区组设计,以减少实验误差。
2.异常值处理
获取并记录试验数据后,需采用一定的策略鉴别和处理异常值,应调查产生异常值的原因。对于技术性或物理性等明确原因导致的异常值可直接剔除,如细胞孔污染、加样错误等;而对没有查明原因的异常值原则上不应剔除,即使剔除也应采用合适的统计学方法。关于异常值剔除的统计学方法及其缺项补足,见本通则“三、量反应平行线测定法”中异常值剔除项。
3.四参数逻辑斯蒂(logistic)模型拟合
一般采用适宜的计算机软件中四参数逻辑斯蒂(logistic)自由模型和约束模型,按照非线性最小二乘法的原则,进行S和T剂量反应曲线的自由拟合和约束拟合,分别获得S和T自由拟合及约束拟合曲线中A、B、C、D四个参数的估计值。约束模型为一平行曲线模型,其中S与T拟合方程的A、B、D三个参数的估计值分别相同,仅参数C的估计值不同。
4.方差分析
按(37)~(39)式将约束模型总变异进行分解,采用适宜的计算机软件计算各项变异的差方和、自由度(f),按(18)式计算各变异项方差。
差方和总=差方和试品间+差方和回归+差方和残差I (37)
差方和残差I=差方和残差Ⅱ+差方和偏离平行 (38)
差方和残差Ⅱ=差方和模型失拟+差方和误差 (39)
上述式中 差方和残差I为标准品和供试品约束模型的残差平方和;
差方和残差Ⅱ为标准品和供试品自由模型的残差平方和。
5.可靠性测验
通过对剂间变异的分析,以测验S和T的对数剂量和反应的关系是否显著偏离平行曲线。剂间变异分析为试品间、回归、偏离平行和模型失拟四项:残差II的方差用以进行试品间、回归和偏离平行三项变异的F测验,误差项的方差用以进行模型失拟的F测验。由适宜的计算机软件计算获得各变异项的P值。当P<0.05或P<0.01,即认为在此检验水准下该项变异有显著意义。
可靠性测验结果 判断可靠性测验结果,回归项应非常显著(P<0.01);偏离平行和模型失拟均应不显著(P≥0.05)。个别情况下,当残差II或误差项的方差非常小时,偏离平行或模型失拟检验结果可能判为显著,建议此时以残差II或误差质控图中日常平均水平替代该次试验水平进行计算。
试品间一项不作为可靠性测验的判断标准。试品间变异非常显著者,重复试验时,应参考所得结果重新估计T的效价或重新调整剂量再进行试验。
满足上述条件,即可认为实验结果的可靠性成立。
6.效价(PT)及置信区间(CL)计算
对于可靠性成立的实验结果,方可按等反应剂量比的原则,采用约束模型中S和T拟合曲线EC50的比值,计算供试品的相对效价(R)。

再按下式计算供试品的效价(PT)
PT=AT・R
采用经验证的适宜计算机软件计算R的置信区间,将R置信区间的高限和低限分别乘以AT得PT置信区间的高限和低限。对于多次实验结果的合并计算见本通则“六、实验结果的合并计算”部分。
在进行本法运算时,选择的计算机软件应能获得与本法实例一致的计算结果。
对符合S形量反应模型的供试品进行效价计算时,如果没有合适的计算机软件或统计专家的帮助,无法使用四参数回归计算法的情况下,也可选择剂量反应曲线中呈近似直线关系的一段剂量范围,将反应值进行适宜转换,按“三、量反应平行线测定法”估计效价。
7.实例
例6 四参数回归计算法
人粒细胞刺激因子(GCSF)生物学活性测定——NFS-60细胞/MTT比色法
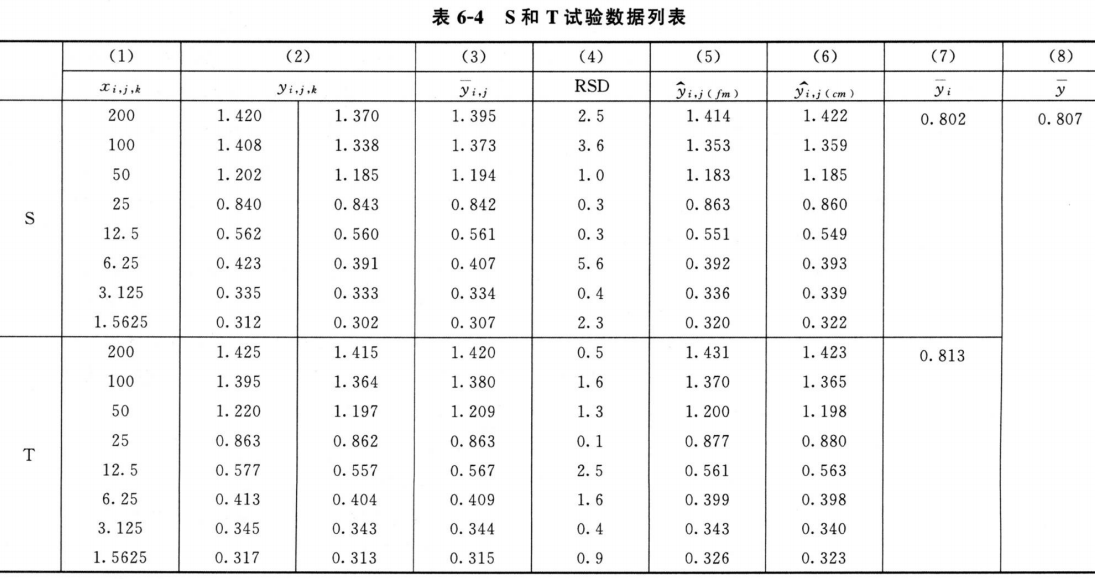
测定方法见人粒细胞刺激因子生物学活性测定法(通则3525)( (通则3525)),试验中将S和T(标示量AT:2.4×107IU/300μg)用基础培养液稀释至每1ml含400IU,然后做2倍系列稀释,共8个稀释度,每个稀释度做2孔,酶标仪吸光度测定结果见表6-1。以yi,j,k表示S或T每一剂量水平的反应值,其中i表示S或T处理组,i=0时为S处理组,i=1时为T处理组;j表示第j个剂量组;k表示每一剂量水平的第k个重复数。
(通则3525)),试验中将S和T(标示量AT:2.4×107IU/300μg)用基础培养液稀释至每1ml含400IU,然后做2倍系列稀释,共8个稀释度,每个稀释度做2孔,酶标仪吸光度测定结果见表6-1。以yi,j,k表示S或T每一剂量水平的反应值,其中i表示S或T处理组,i=0时为S处理组,i=1时为T处理组;j表示第j个剂量组;k表示每一剂量水平的第k个重复数。
(1)四参数逻辑斯蒂(logistic)模型拟合
采用适宜的计算机软件中四参数逻辑斯蒂(logistic)自由模型对表6-1中的数据进行S和T剂量反应曲线的拟合,其决定系数R2分别为0.997和0.999,S和T自由模型拟合曲线中A、B、C、D四个参数的估计值见表6-2。

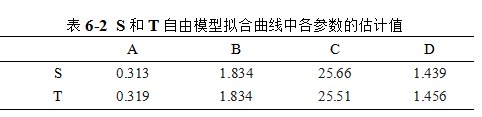
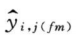
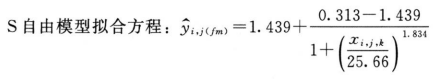
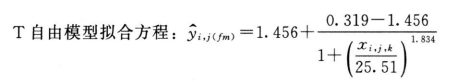
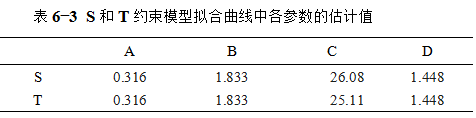
再采用适宜的计算机软件中四参数logistic约束模型对表6-1中的数据进行S和T剂量反应曲线的拟合,S和T约束模型拟合曲线中A、B、C、D四个参数的估计值见表6-3。
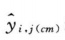
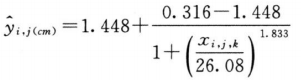
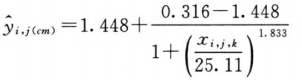
(2)方差分析

将总变异进行分解,计算各项变异的差方和与自由度(f)。
总变异
差方和总=(1.420-0.807)2+•••+(0.302-0.807)2+(1.425-0.807)2+•••+(0.313-0.807)2=6.10858
f总=2×8×2-1=31
试品间变异
差方和试品间=2×8×[(0.802-0.807)2+(0.813-0.807)2]=0.00108
f试品间=2-1=1
回归项变异
差方和回归=[(1.422-0.802)2+•••+(0.322-0.802)2+(1.423-0.813)2+•••+(0.323-0.813)2]×2
=6.09729
f回归=5-2=3
偏离平行项变异
差方和偏离平行=[(1.420-1.422)2+•••+(0.302-0.322)2+(1.425-1.423)2+•••+(0.313-0.323)2]-[(1.420-1.414)2+•••+(0.302-0.320)2+(1.425-1.431)2+•••+(0.313-0.326)2]=4.468E-04
f偏离平行=8-5=3
残差Ⅱ变异
差方和残差Ⅱ=(l.420-1.414)2+•••+(0.302-0.320)2+(1.425-1.431)2+•••+(0.313-0.326)2=0.01052
f残差Ⅱ=2×8×2-8=24
①失拟项变异
差方和模型失拟=2×[(1.395-1.414)2+•••+(0.307-0.320)2+(1.420-1.431)2+•••+(0.315-0.326)2]=0.00505
f模型失拟=2×8-8=8
标准品失拟项变异:
差方和标准品模型失拟=2×[(l.395-1.414)2+•••+(0.307-0.320)2]=0.00360
f标准品模型失拟=8-8/2=4
供试品失拟项变异:
差方和供试品模型失拟=2×[(1.420-1.431)2+•••+(0.315-0.326)2]=0.00145
f供试品模型失拟=8-8/2=4
②误差项变异
差方和误差=0.010517-5.056E-03=0.00546
f误差=2×8×2-2×8=16
(3)可靠性测验
按本通则“三、量反应平行线测定法”中(18)式计算各变异项方差,将方差分析结果列表进行F测验,见表6-5。
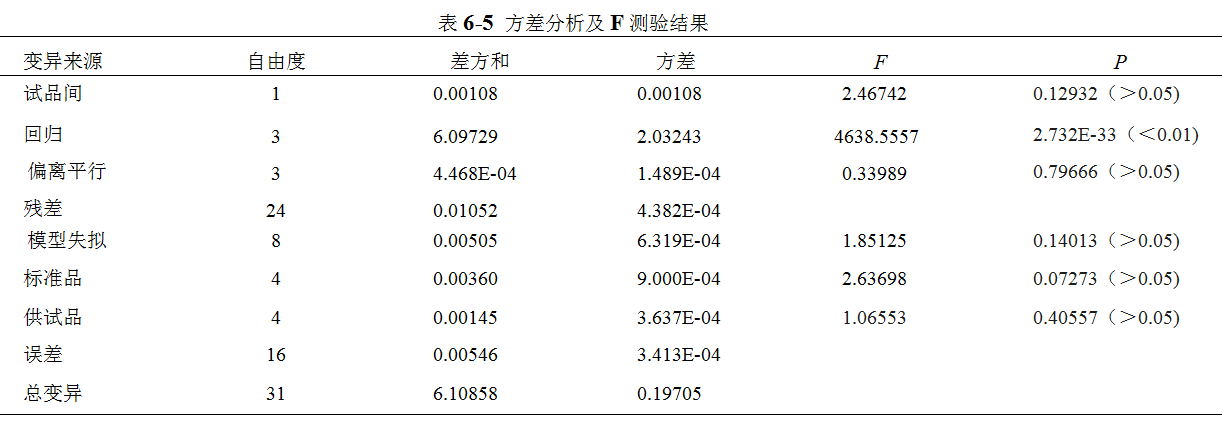
注:表中残差为残差Ⅱ。
可靠性测验结果判断 根据历史数据设定S和T拟合曲线R2应≥0.98,每一剂量组反应值的RSD应≤10%。可靠性测验结果判断如下:
①S和T拟合曲线的R2分别为0.997和0.999,均符合规定。
②S和T每一剂量组内反应值的RSD均<10%,均符合规定。
③回归项非常显著;偏离平行和失拟检验项均不显著。
结论:实验结果成立。
(4)效价(PT)及置信区间计算
相对效价(R)按约束模型中S和T拟合曲线EC50(见表6-3中C值)的比值计算。
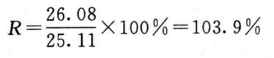
再按下式计算供试品效价:
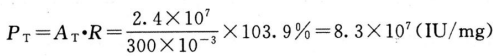
采用适宜的计算机软件,计算R的置信区间为98.3%~109.7%,PT的置信区间为(7.9~8.8)×107IU/mg,R和PT的相对置信区间均为94.6%~105.6%。
五、质反应的生物实验数据分析
某些无法定量测量的检验,每个试验单位只有二分的测量结果,例如观察到动物的存活或死亡,细胞的响应超过或未超过预设的限度等。处理该类检验适用于质反应测定法。
质反应测定法与量反应测定法的区别在于,在每个剂量下的n次独立重复测量仅得到一个单一的值,即响应比例。将对数剂量对响应比例作图,通常将得到S形的剂量响应曲线。该曲线通常可以通过累积正态分布函数表示。使用累积正态分布函数的模型通常称为概率单位(probit)模型,使用逻辑斯蒂分布函数的模型通常称为logit模型,两者计算结果不存在有意义的差异,均可接受。常用Bliss迭代法计算模型参数。
1.概率单位(probit)转换的平行线法
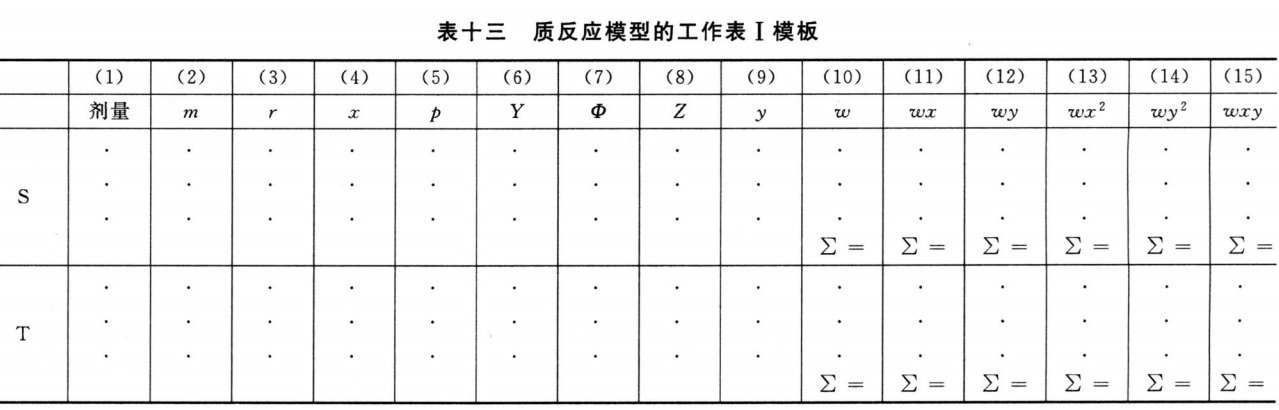
(1)将实验数据输入工作表Ⅰ(表十三),按工作表Ⅰ和工作表Ⅱ的循环迭代计算 首先将试验数据输入工作表Ⅰ以下数字标识的各列。
列(1)为标准品或供试品的剂量。
列(2)为该剂量下的单位数m。
列(3)为该剂量下产生阳性响应的单位数r。
列(4)为对数剂量x。
列(5)为每组阳性响应的比例p=r/m。
从列(6)开始,循环迭代计算结果:
列(6)第一个循环时,列Y全部填写0。
列(7)累积标准正态分布方程对应的值Φ=Φ(Y)。
工作表Ⅰ的列(8)到列(10)用以下公式计算。
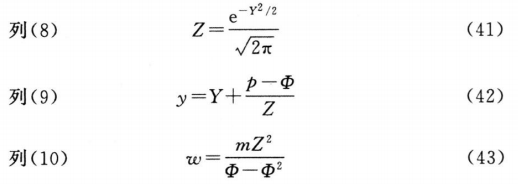
工作表I的列(11)到列(15)的ωx、ωy、ωx2、ωy2和ωxy可以由该表的列(4)、(9)和(10)算得,对每供试品和标准品分别计算列(10)~(15)各列之和(∑)。
将工作表I计算得到的求和转移至工作表II(表十四)中的列(1)~(6),通过以下公式计算工作表II列(7)~(11)。
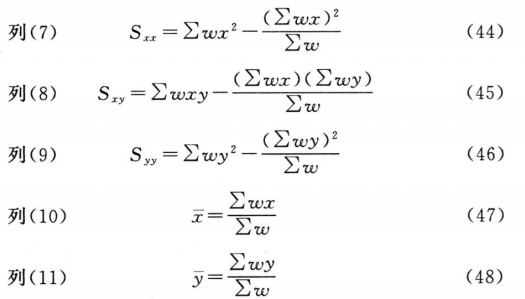

供试品和标准品的共同斜率参数b以(49)式计算:
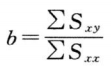
供试品和标准品的截距参数a以(50)式计算,并填入工作表II的列(12):


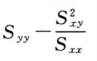
对工作表II列(13)的计算结果求和得到χ2值,以自由度f=K-2h查χ2表(k=dh,d为每个测试品的浓度值;h为总的测试品数目,只有一个标准品和一个供试品,则h=2),可得到尾区概率P。当P<0.05或P<0.01,即为在此概率水平下对偏离线性有显著意义。
偏离平行性的程度可以通过以下方法测量。工作表II中的数据通过(52)式计算得到χ2值,以自由度f=h-1查χ2表,可得到尾区概率P。当P<0.05或P<0.01,即为在此概率水平下对平行性的偏离有显著意义。
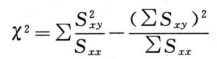
可靠性检验结果,偏离线性和平行性应不显著(P>0.05)。显著偏离线性应当复试。实验者在剂量设置时应当尽可能保证S和T的对数剂量均覆盖各自S形曲线半数反应量的两侧,即最低稀释度有半数以上的动物响应,最高稀释度有半数以下的动物响应。同时,S和T曲线的水平距离应当尽可能小,以充分保证拟合的稳健性和检验结果的可靠性。
显著偏离线性应当复试,但如果有理由保留该检验,公式需要微调。(56)式中的t应当修正为偏离线性检验中相同自由度f=K-2h对应的P=0.05处的t值,s2应当修正为偏离线性检验中的χ2值除以自由度f=K-2h。
同时,平行性检验也需要微调。偏离平行性检验的χ2值除以自由度f=h-1后,再除以上述计算得到的s2,得到一个F比率值,分子和分母分别对应自由度f=h-1和f=K-2h,在0.05的显著水平上进行F检验以判断平行性。

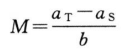
式中aT为供试品的截距参数,aS为标准品的截距参数。
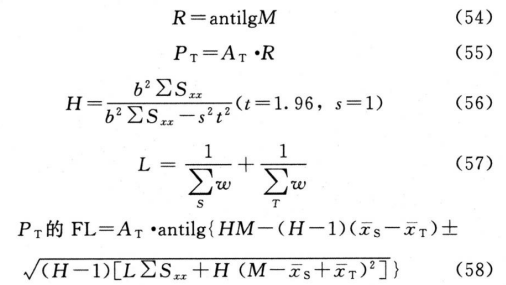
2.半数反应量计算
半数反应量包括半数有效量(ED50或IC50)和半数致死量(LD50)等,是衡量药物有效性和安全性的常用指标,在质反应测定法中,表现为百分之五十单位响应时的剂量。供试品的半数反应量常用prob
继续阅读
在线查询结果来源于2020年版中国药典,仅供参考。由专业团队进行审核校对。

